算法 - (数组)

func lengthOfLongestSubstring(s string) int {
	if len(s) == 0 {
		return 0
	}

	checkFunc := func(sub string) bool {
		m := make(map[byte]struct{})
		for i := 0 ; i < len(sub); i++ {
			if _, ok := m[sub[i]]; ok {
				return false
			} else {
				m[sub[i]] = struct{}{}
			}
		}
		return true
	}

	maxLength := 1
	for i := 0; i < len(s); i++ {
		for j := i; j < len(s); j ++ {
			subStr := s[i:j+1]
			if checkFunc(subStr) {
				if len(subStr) > maxLength {
					maxLength = len(subStr)
				}
			}
		}
	}
	return maxLength
}

func lengthOfLongestSubstring(s string) int {
	right := 0
	// 用于存当前窗口中都有哪些字符，当map的value不为1时，表示需要滑动了
	storeMap := make(map[byte]int)
	max := 0

	for left := 0; left < len(s); left++ {
        // 左指针向前移动一下，消除窗口中的重复值
		if left != 0 {
			delete(storeMap, s[left-1])
		}
		for ; right < len(s); right++ {
			// 为0表示是新元素
			if storeMap[s[right]] == 0 {
				storeMap[s[right]]++
			} else {
				break
			}
		}
		// 窗口中存在重复字符串了(或者遍历完了数组), 且肯定出现的重复字符是最早加入的（left所指的值）
		if max < right-left {
			max = right - left
		}
	}

	return max
}

func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
	// 确保nums1是较短的数组
	if len(nums1) > len(nums2) {
		nums1, nums2 = nums2, nums1
	}
	
	m, n := len(nums1), len(nums2)
	left, right := 0, m
	
	for left <= right {
		// nums1的分割点
		i := (left + right) / 2
		// nums2的分割点，保证左半部分元素总数 = (m+n+1)/2
		j := (m+n+1)/2 - i
		
		// 边界值处理
		maxLeft1 := -1<<31 // 负无穷
		if i > 0 {
			maxLeft1 = nums1[i-1]
		}
		
		minRight1 := 1<<31 - 1 // 正无穷
		if i < m {
			minRight1 = nums1[i]
		}
		
		maxLeft2 := -1<<31 // 负无穷
		if j > 0 {
			maxLeft2 = nums2[j-1]
		}
		
		minRight2 := 1<<31 - 1 // 正无穷
		if j < n {
			minRight2 = nums2[j]
		}
		
		// 检查分割是否正确
		if maxLeft1 <= minRight2 && maxLeft2 <= minRight1 {
			// 找到正确的分割
			if (m+n)%2 == 0 {
				// 总长度为偶数
				return float64(max(maxLeft1, maxLeft2)+min(minRight1, minRight2)) / 2.0
			} else {
				// 总长度为奇数
				return float64(max(maxLeft1, maxLeft2))
			}
		} else if maxLeft1 > minRight2 {
			// nums1分割点太靠右
			right = i - 1
		} else {
			// nums1分割点太靠左
			left = i + 1
		}
	}
	
	return 0.0
}

func longestPalindrome(s string) string {
	if len(s) <= 1 {
		return s
	}
	longestStr := ""

	for i := 0; i < len(s); i++ {
		str1 := helper(s, i, i+1)  // 考虑 abba 形式
		str2 := helper(s, i, i)    // 考虑 aba 形式
		if len(longestStr) < len(str1) {
			longestStr = str1
		}
		if len(longestStr) < len(str2) {
			longestStr = str2
		}
	}

	return longestStr
}

// 查找最长子串
func helper(s string, left, right int) string {
	var str string
	for ; left >= 0 && right <= len(s)-1 && s[left] == s[right]; left, right = left-1, right+1 {
		str = s[left : right+1]
	}
	return str
}

func maxArea(height []int) int {
	maxV := 0
	left, right := 0, len(height)-1
	
	for left < right {
		if height[left] > height[right] {
			maxV = max((right-left) * height[right], maxV)
			// 左边更高，右边左移
			right -- 
		} else {
			maxV = max((right-left) * height[left], maxV)
			// 右边更高，左边右移动
			left ++ 
		}
	}
	
	return maxV
}

func threeSum(nums []int) [][]int {
	sort.Ints(nums)

	validNums := make(map[[3]int]struct{})

	for i := 0; i < len(nums)-2; i++ {
		minNum := nums[i]
		midNumIndex := i + 1
		maxNumIndex := len(nums) - 1
		// 中间索引 小于 最大索引
		for midNumIndex < maxNumIndex {
			midNum := nums[midNumIndex]
			maxNum := nums[maxNumIndex]
			// 大于0了，证明最大的数太大了
			if minNum+midNum+maxNum > 0 {
				maxNumIndex--
				continue
			}
			// 小于0了，证明中间数太小了
			if minNum+midNum+maxNum < 0 {
				midNumIndex++
				continue
			}
			// 只能是等于 0 了, 中间数加点，最大数减点，看看是否还能拼出0
			if minNum+midNum+maxNum == 0 {
				validNums[[3]int{minNum, midNum, maxNum}] = struct{}{}
				midNumIndex++
				maxNumIndex--
			}
		}
	}

	var res [][]int
	for k, _ := range validNums {
		res = append(res, []int{k[0], k[1], k[2]})
	}

	return res
}

func letterCombinations(digits string) []string {
   if len(digits) == 0 {
       return []string{}
   }
   
   mapping := map[byte]string{
       '2': "abc", '3': "def", '4': "ghi", '5': "jkl",
       '6': "mno", '7': "pqrs", '8': "tuv", '9': "wxyz",
   }
   
   var result []string
   var backtrack func(index int, path string)
   
   backtrack = func(index int, path string) {
       if index == len(digits) {
           result = append(result, path)
           return
       }
       
       for _, char := range mapping[digits[index]] {
           backtrack(index+1, path+string(char))
       }
   }
   
   backtrack(0, "")
   return result
}

package main

import "fmt"

func isValid(s string) bool {
	stack := []rune{}
	mapping := map[rune]rune{
		')': '(',
		'}': '{',
		']': '[',
	}
	
	for _, char := range s {
		if char == '(' || char == '{' || char == '[' {
			// 左括号入栈
			stack = append(stack, char)
		} else {
			// 右括号
			if len(stack) == 0 {
				return false
			}
			// 检查栈顶是否匹配
			if stack[len(stack)-1] != mapping[char] {
				return false
			}
			// 匹配成功，出栈
			stack = stack[:len(stack)-1]
		}
	}
	
	// 栈为空说明所有括号都匹配
	return len(stack) == 0
}

func removeDuplicates(nums []int) int {
	if len(nums) == 0 {
		return 0
	}

	slow := 1
	for fast := 1; fast < len(nums); fast++ {
		if nums[fast] != nums[fast-1] {
			nums[slow] = nums[fast]
			slow++
		}
	}

	return slow
}

func reversal(nums []int) {
	length := len(nums)
	for i := 0; length > 1 && i < length/2; i ++ {
		nums[i],nums[length-1-i] = nums[length-1-i],nums[i]
	}
}

func removeDuplicates(nums []int) int {
	length := len(nums)

	for i := 0; i < length; i ++ {
		if i + 1 < length && nums[i] == nums[i+1] {
			reversal(nums[i+1:length])
			reversal(nums[i+1:length-1])
			length = length - 1
			i = i - 1
		}
	}
	return length
}

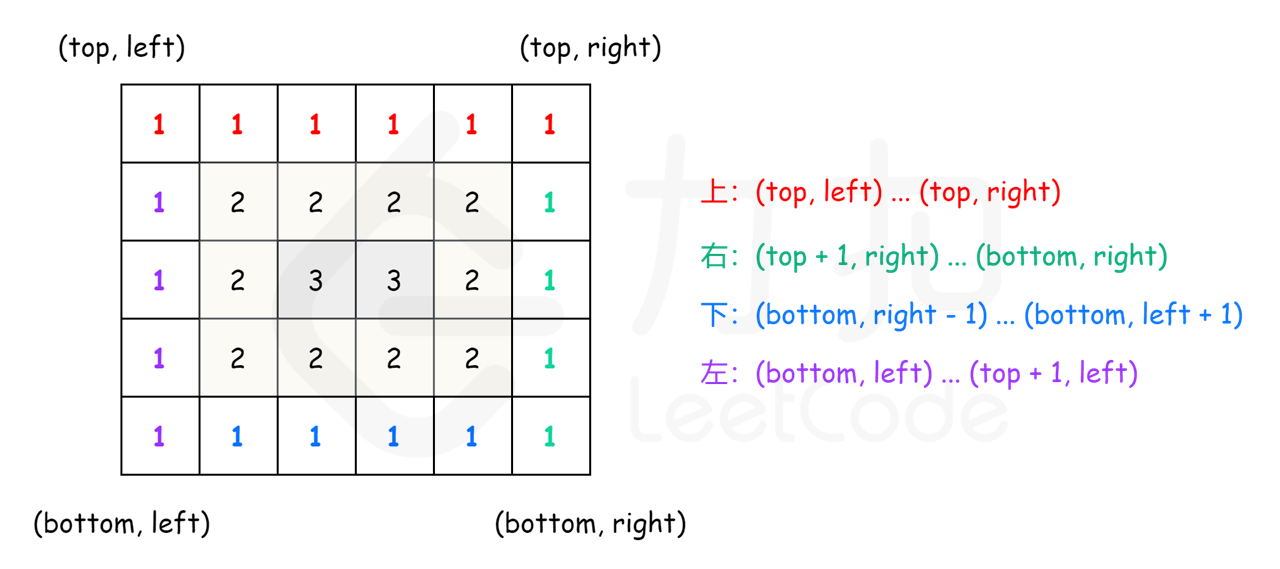
func spiralOrder(matrix [][]int) []int {
	if len(matrix) == 0 || len(matrix[0]) == 0 {
		return []int{}
	}

	var (
		rows, columns = len(matrix), len(matrix[0])
		order = make([]int, rows * columns)
		index = 0
		left, right, top, bottom = 0, columns -1 , 0 , rows -1
	)

	for left <= right && top <= bottom {
		// 打印最上层(包含top行最后一个)
		for col := left; col <= right; col ++ {
			order[index] = matrix[top][col]
			index++
		}
		// 打印最右边(包含最右列最后一个)
		for row := top + 1; row <= bottom; row ++ {
			order[index] = matrix[row][right]
			index++
		}
		//
		if left < right && top < bottom {
			// 打印最下边(不包含bottom行最后一个和第一个)
			for col := right - 1; col > left; col -- {
				order[index] = matrix[bottom][col]
				index++
			}
			// 打印最左边(不包含left列最后一个)
			for row := bottom; row > top; row -- {
				order[index] = matrix[row][left]
				index++
			}
		}
	}
	left ++
	right --
	top ++
	bottom --

	return order
}

//一次二分查找 + 扩展
func searchRangeExpand(nums []int, target int) []int {
	if len(nums) == 0 {
		return []int{-1, -1}
	}
	
	// 先用标准二分查找找到任意一个target的位置
	pos := binarySearch(nums, target)
	if pos == -1 {
		return []int{-1, -1}
	}
	
	// 从找到的位置向两边扩展
	left, right := pos, pos
	
	// 向左扩展
	for left > 0 && nums[left-1] == target {
		left--
	}
	
	// 向右扩展
	for right < len(nums)-1 && nums[right+1] == target {
		right++
	}
	
	return []int{left, right}
}

func binarySearch(nums []int, target int) int {
	left, right := 0, len(nums)-1
	
	for left <= right {
		mid := left + (right-left)/2
		
		if nums[mid] == target {
			return mid
		} else if nums[mid] < target {
			left = mid + 1
		} else {
			right = mid - 1
		}
	}
	
	return -1
}

func combinationSum(candidates []int, target int) [][]int {
	result := [][]int{}
	current := []int{}
	var backtrack func(start int, remain int)

	backtrack = func(start int, remain int) {
		if remain < 0 {
			return
		}
		if remain == 0 {
			temp := make([]int, len(current))
			copy(temp, current)
			result = append(result, temp)
			return
		}

		for i := start; i < len(candidates); i++ {
			// 选择
			current = append(current, candidates[i])
			// 递归
			backtrack(i, remain-candidates[i])
			// 回溯
			current = current[:len(current)-1]
		}
	}

	backtrack(0, target)
	return result
}

func trap(height []int) int {
	if len(height) <= 2 {
		return 0
	}

	// 初始化左右指针
	left, right := 0, len(height)-1
	// 初始化左右最大高度
	leftMax, rightMax := 0, 0
	// 初始化雨水总量
	totalWater := 0

	for left < right {
		// 更新左边的最大高度
		if height[left] > leftMax {
			leftMax = height[left]
		} 
		if height[right] > rightMax {
			rightMax = height[right]
		}

		// 根据短板决定处理那一侧
		if leftMax <= rightMax {
			// 左边是短板，计算左边的雨水量
			totalWater += leftMax - height[left]
			left ++
		} else {
			// 右边是短板，计算右边的雨水量
			totalWater += rightMax - height[right]
			right -- 
		}
	}

	return totalWater
}

type PermState struct {
	nums        []int        // 输入数组
	currentPerm []int        // 当前正在构建的排列
	usedNums    map[int]bool // 标记哪些数字在使用
	allPerms    [][]int      // 存储所有完成的排列
}

func NewPermState(nums []int) *PermState {
	return &PermState{
		nums:        nums,
		currentPerm: []int{},
		usedNums:    make(map[int]bool),
		allPerms:    make([][]int, 0),
	}
}

func (ps *PermState) Add(i int) {
	ps.currentPerm = append(ps.currentPerm, ps.nums[i])
	ps.usedNums[i] = true 
}

func (ps *PermState) Remove(i int) {
	ps.currentPerm = ps.currentPerm[:len(ps.currentPerm)-1]
	ps.usedNums[i] = false
}

func (ps *PermState) CanUse(i int) bool {
	return !ps.usedNums[i]
}

func (ps *PermState) IsComplete() bool {
	return len(ps.currentPerm) == len(ps.nums)
}

func (ps *PermState) Save() {
	temp := make([]int, len(ps.currentPerm))
	copy(temp, ps.currentPerm)
	ps.allPerms = append(ps.allPerms, temp)
}

func (ps *PermState) BuildPerm() {
	if ps.IsComplete() {
		ps.Save()
		return 
	}
	
	for i := 0; i < len(ps.nums); i ++ {
		if ps.CanUse(i) {
			ps.Add(i)
			ps.BuildPerm()
			ps.Remove(i)
		}
	}
}

func permute(nums []int) [][]int {
	ps := NewPermState(nums)
	ps.BuildPerm()
	return ps.allPerms
}

func rotate(matrix [][]int) {
	n := len(matrix)
	
	// 第一步：转置矩阵 (沿主对角线翻转)
	for i := 0; i < n; i++ {
		for j := i + 1; j < n; j++ {
			matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
		}
	}
	
	// 第二步：反转每一行
	for i := 0; i < n; i++ {
		left, right := 0, n-1
		for left < right {
			matrix[i][left], matrix[i][right] = matrix[i][right], matrix[i][left]
			left++
			right--
		}
	}
}

func groupAnagrams(strs []string) [][]string {
	anagramMap := make(map[string][]string)

	for _, str := range strs {
		// 将字符串转换为 rune 切片并排序
		sorted := sortString(str)
		// 按排序后的字符串作为 key 存入 map
		anagramMap[sorted] = append(anagramMap[sorted], str)
	}

	// 收集结果
	result := make([][]string, 0, len(anagramMap))
	for _, group := range anagramMap {
		result = append(result, group)
	}

	return result
}

// sortString 对字符串按字典序排序
func sortString(s string) string {
	runes := strings.Split(s, "")
	sort.Strings(runes)
	return strings.Join(runes, "")
}

// merge 合并重叠的区间
func merge(intervals [][]int) [][]int {
	// 边界情况处理
	if len(intervals) <= 1 {
		return intervals
	}
	
	// 按照区间起始位置排序
	sort.Slice(intervals, func(i, j int) bool {
		return intervals[i][0] < intervals[j][0]
	})
	
	// 初始化结果数组，将第一个区间加入
	result := [][]int{intervals[0]}
	
	// 遍历剩余区间
	for i := 1; i < len(intervals); i++ {
		current := intervals[i]
		last := result[len(result)-1]
		
		// 如果当前区间与最后一个合并区间重叠
		if current[0] <= last[1] {
			// 合并区间：更新结束位置为两者的最大值
			last[1] = max(last[1], current[1])
		} else {
			// 不重叠，直接添加当前区间
			result = append(result, current)
		}
	}
	
	return result
}

// 滑动窗口 + 哈希表
func minWindow(s string, t string) string {
	if len(s) == 0 || len(t) == 0 || len(s) < len(t) {
		return ""
	}
	
	// 统计t中每个字符需要的数量
	need := make(map[byte]int)
	for i := 0; i < len(t); i++ {
		need[t[i]]++
	}
	
	// 窗口中字符的数量
	window := make(map[byte]int)
	
	left, right := 0, 0
	valid := 0 // 窗口中满足need条件的字符个数
	
	// 记录最小覆盖子串的起始索引及长度
	start, length := 0, len(s)+1
	
	for right < len(s) {
		// 扩大窗口
		c := s[right]
		right++
		
		// 进行窗口内数据的一系列更新
		if _, exists := need[c]; exists {
			window[c]++
			if window[c] == need[c] {
				valid++
			}
		}
		
		// 判断左侧窗口是否要收缩
		for valid == len(need) {
			// 更新最小覆盖子串
			if right-left < length {
				start = left
				length = right - left
			}
			
			// 缩小窗口
			d := s[left]
			left++
			
			// 进行窗口内数据的一系列更新
			if _, exists := need[d]; exists {
				if window[d] == need[d] {
					valid--
				}
				window[d]--
			}
		}
	}
	
	if length == len(s)+1 {
		return ""
	}
	return s[start : start+length]
}

func subsets(nums []int) [][]int {
	result := [][]int{}
	current := []int{}
	var backtrack func(start int)
	
	backtrack = func(start int) {
		// 将当前子集添加到结果中
		temp := make([]int, len(current))
		copy(temp, current)
		result = append(result, temp)
		
		// 递归生成所有子集
		for i := start; i < len(nums); i++ {
			// 选择当前元素
			current = append(current, nums[i])
			// 递归生成以当前元素为基础的子集
			backtrack(i + 1)
			// 回溯，撤销选择
			current = current[:len(current)-1]
		}
	}
	
	backtrack(0)
	return result
}

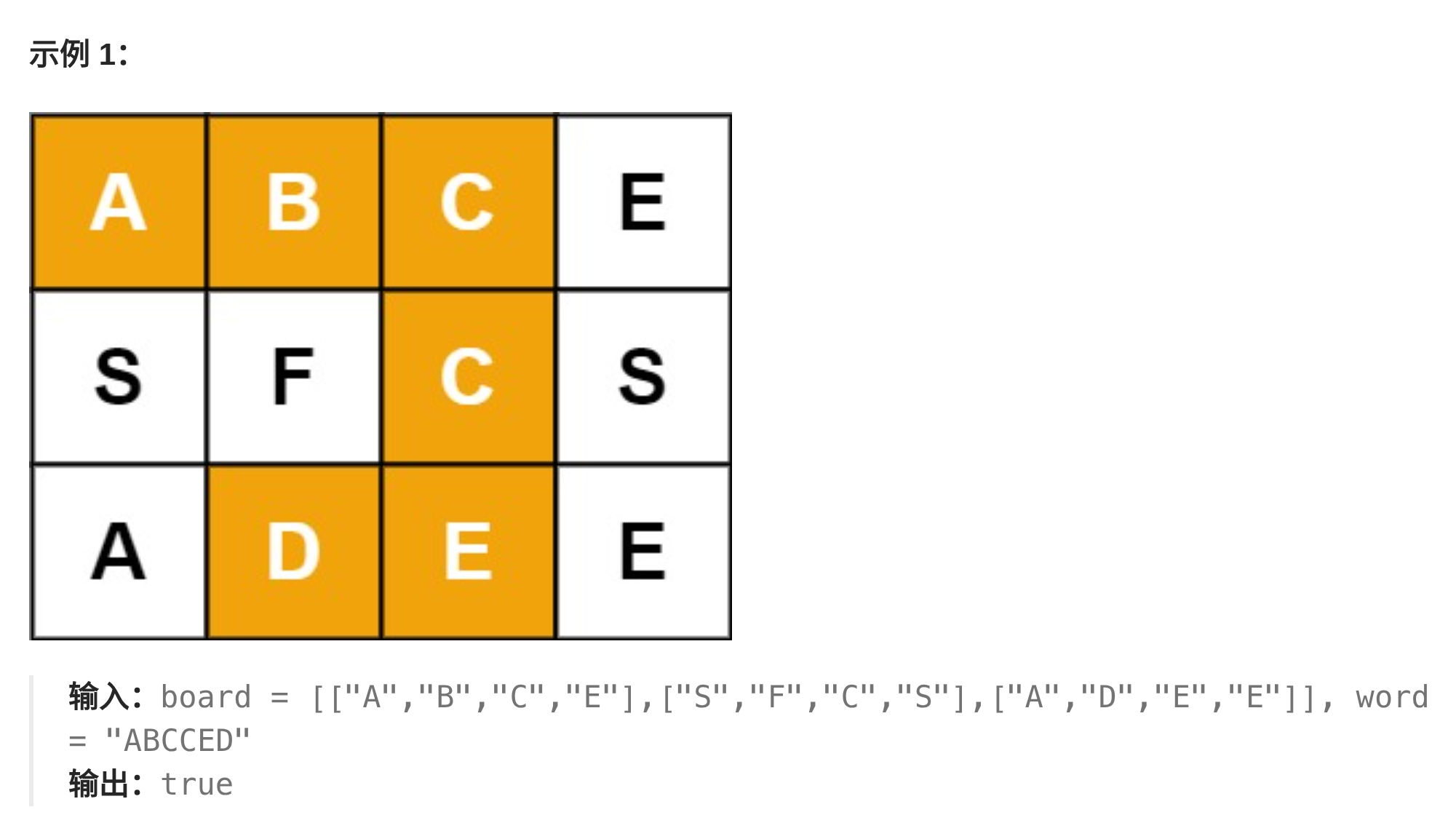
func exist(board [][]byte, word string) bool {
	m := len(board)
	if m == 0 {
		return false
	}
	n := len(board[0])
	if n == 0 {
		return false
	}
	
	for i := 0; i < m; i++ {
		for j := 0; j < n; j++ {
			if backtrack(board, word, i, j, 0) {
				return true
			}
		}
	}
	
	return false
}

func backtrack(board [][]byte, word string, row, col, k int) bool {
	// 边界条件检查，如果索引越界或字符不匹配，返回 false
	if row < 0 || row >= len(board) || col < 0 || col >= len(board[0]) || board[row][col] != word[k] {
		return false
	}
	
	// 如果所有字符都匹配完毕，说明找到了完整的单词
	if k == len(word)-1 {
		return true
	}
	
	// 临时标记当前单元格，防止重复使用
	temp := board[row][col]
	board[row][col] = '#'
	
	// 递归搜索四个相邻方向
	// 上
	if backtrack(board, word, row-1, col, k+1) {
		return true
	}
	// 下
	if backtrack(board, word, row+1, col, k+1) {
		return true
	}
	// 左
	if backtrack(board, word, row, col-1, k+1) {
		return true
	}
	// 右
	if backtrack(board, word, row, col+1, k+1) {
		return true
	}
	
	// 回溯：恢复当前单元格
	board[row][col] = temp
	
	return false
}

func majorityElement(nums []int) int {
	if len(nums) == 0 {
		return 0
	}
	if len(nums) == 1 {
		return nums[0]
	}
	major := nums[0]
	count := 1
	for i := 1; i < len(nums); i++ {
		if nums[i] == major {
			count++
		} else {
			count--
		}
		if count < 0 {
			count = 1
			major = nums[i]
		}
	}
	count = 0
	for i := 0; i < len(nums); i++ {
		if major == nums[i] {
			count += 1
		}
	}
	if count >= len(nums)/2 {
		return major
	}
	return 0
}

func longestConsecutive(nums []int) int {
	if len(nums) == 0 {
		return 0
	}
	
	// 使用map模拟set，存储所有数字
	numSet := make(map[int]bool)
	for _, num := range nums {
		numSet[num] = true
	}
	
	maxLength := 0
	
	// 遍历每个数字
	for num := range numSet {
		// 只从连续序列的起始点开始计算
		if !numSet[num-1] {
			currentNum := num
			currentLength := 1
			
			// 向右延伸，找连续的数字
			for numSet[currentNum+1] {
				currentNum++
				currentLength++
			}
			
			// 更新最大长度
			if currentLength > maxLength {
				maxLength = currentLength
			}
		}
	}
	
	return maxLength
}

// 双向链表节点
type Node struct {
	key, value int
	prev, next *Node
}

type LRUCache struct {
	capacity int
	cache    map[int]*Node
	head     *Node // 虚拟头节点
	tail     *Node // 虚拟尾节点
}

func Constructor(capacity int) LRUCache {
	lru := LRUCache{
		capacity: capacity,
		cache:    make(map[int]*Node),
		head:     &Node{},
		tail:     &Node{},
	}
	// 初始化双向链表
	lru.head.next = lru.tail
	lru.tail.prev = lru.head
	return lru
}

// 添加节点到头部
func (lru *LRUCache) addToHead(node *Node) {
	node.prev = lru.head
	node.next = lru.head.next
	lru.head.next.prev = node
	lru.head.next = node
}

// 移除节点
func (lru *LRUCache) removeNode(node *Node) {
	node.prev.next = node.next
	node.next.prev = node.prev
}

// 移动节点到头部
func (lru *LRUCache) moveToHead(node *Node) {
	lru.removeNode(node)
	lru.addToHead(node)
}

// 移除尾部节点
func (lru *LRUCache) removeTail() *Node {
	lastNode := lru.tail.prev
	lru.removeNode(lastNode)
	return lastNode
}

func (lru *LRUCache) Get(key int) int {
	if node, exists := lru.cache[key]; exists {
		// 移动到头部表示最近使用
		lru.moveToHead(node)
		return node.value
	}
	return -1
}

func (lru *LRUCache) Put(key int, value int) {
	if node, exists := lru.cache[key]; exists {
		// 更新值并移动到头部
		node.value = value
		lru.moveToHead(node)
	} else {
		newNode := &Node{key: key, value: value}
		
		if len(lru.cache) >= lru.capacity {
			// 超出容量，删除尾部节点
			tail := lru.removeTail()
			delete(lru.cache, tail.key)
		}
		
		// 添加新节点到头部
		lru.cache[key] = newNode
		lru.addToHead(newNode)
	}
}

func majorityElement(nums []int) int {
	candidate := 0
	count := 0
	
	// 第一遍：找候选人
	for _, num := range nums {
		if count == 0 {
			candidate = num
		}
		
		if num == candidate {
			count++
		} else {
			count--
		}
	}
	
	// 由于题目保证存在多数元素，这里可以直接返回candidate
	// 如果不保证，需要第二遍验证
	return candidate
}

func numIslands(grid [][]byte) int {
	if len(grid) == 0 || len(grid[0]) == 0 {
		return 0
	}
	
	rows, cols := len(grid), len(grid[0])
	count := 0
	
	// DFS函数，将相连的陆地标记为已访问
	var dfs func(int, int)
	dfs = func(i, j int) {
		// 边界检查和水域检查
		if i < 0 || i >= rows || j < 0 || j >= cols || grid[i][j] == '0' {
			return
		}
		
		// 标记为已访问
		grid[i][j] = '0'
		
		// 递归访问四个方向
		dfs(i-1, j) // 上
		dfs(i+1, j) // 下
		dfs(i, j-1) // 左
		dfs(i, j+1) // 右
	}
	
	// 遍历整个网格
	for i := 0; i < rows; i++ {
		for j := 0; j < cols; j++ {
			if grid[i][j] == '1' {
				count++
				dfs(i, j) // 将整个岛屿标记为已访问
			}
		}
	}
	
	return count
}

func minSubArrayLen(target int, nums []int) int {
	ri := 0  // 右指针
	minLength := math.MaxInt  

	if len(nums) == 0 {
		return 0
	}

	curSize := 0

	// 移动左指针
	for i := 0 ; i < len(nums); i ++ {
		if i != 0 { 
			curSize -= nums[i-1]
		}
		
		// 移动右指针。当前Size >= target就退出
		for ri < len(nums) && nums[ri] + curSize < target {
			curSize += nums[ri]
			ri ++
		}
        // 是我们想要的退出时机，而不是ri遍历完了
		if ri < len(nums) && curSize + nums[ri] >= target {
			if ri + 1 - i < minLength {
				minLength = ri + 1 -i
			}
		}
	}
	if minLength == math.MaxInt {
		return 0
	}

	return minLength
}

func minSubArrayLen(target int, nums []int) int {
	var count int = math.MaxInt64
	var targetList []int
	var right int

	for left := 0; left < len(nums); left++ {

		// 持续移动窗口的左边，直到窗口中的数组之和不满足和大于target
		for len(targetList) > 0 {
			// 找到最小
			if sum(targetList) >= target && len(targetList) <= count {
				count = len(targetList)
			} else {
				break
			}
			// 逐渐左移下标
			targetList = targetList[1:]
		}

		// 移动滑动窗口的右边界
		for ; right < len(nums); right++ {
			targetList = append(targetList, nums[right])
			if sum(targetList) < target {
				continue
			} else {
				// 能到这里表示滑动窗口里的值是满足要求的，右指针再往右一格
				if len(targetList) <= count {
					count = len(targetList)
				}
				right++
				break
			}
		}
	}

	if count == math.MaxInt64 {
		return 0
	}

	return count
}

func sum(list []int) int {
	all := 0
	for _, v := range list {
		all += v
	}
	return all
}