算法笔记-稳定匹配算法(Gale-Shapley)
最近工作中遇到一个场景,需要将两种资源做匹配分发,希望动态的做到最佳分配的状态,而且分配的结果需要稳定,刚好了解到这类的算法,特此记录一下。
问题起源
盖尔-沙普利算法(Gale-Shapley) 简称 “GS 算法”,是 1962 年,经济学家 David Gale 和 Lloyd Shapley 为了寻找一个稳定的匹配而设计出的市场机制。这类问题就可以成为稳定匹配问题。一个经典的例子就是 男女找对象。
Stable Matching
假设有一家交友公司,现在有 100 位男生👦 和 100 位女生 👧 需要找对象,所有的男生和女生都需要对异性进行好感度排序 💞,且必须所有人都匹配到,不能有落单的情况,而且不能重复匹配的情况,我们需要最后所有的男生或女生都能得到 Happy 并且 Stable 的对象。

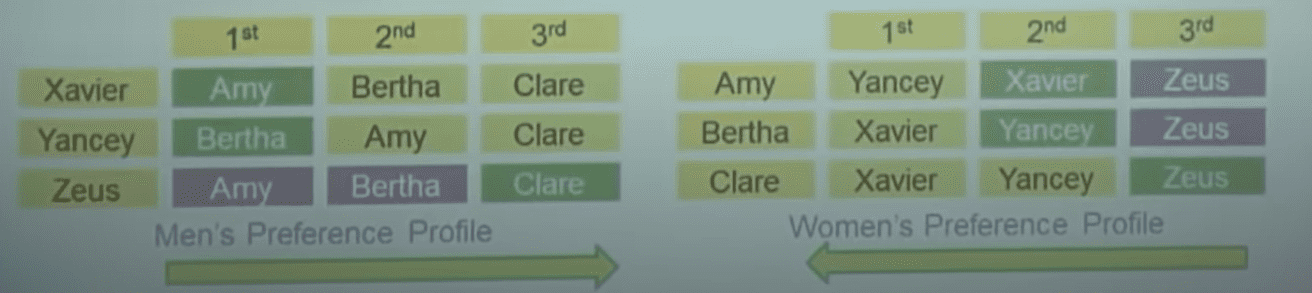
现在假设 有 X、Y 和 Z 男生 与 A、B 和 C 女生。他们心目中的对象排序如上图所示。下面就应该进行 Stable Matching 了,目标是配对完成之后,每个人都是尽可能 Happy 且 Stable 的。
Gale-Shapley Algorithm
寻找稳定匹配问题采用的方法是 Gale-Shapley 算法,这个算法的演算机制简单的说,每次迭代中,男生向女生求婚,而女生有权利拒绝或者接受,但是女生当下的接受或拒绝不是代表最终的结果(deferred decision making),这整个算法的演算过程中有三个阶段
- Free (自由之身)
- Engaged(订婚状态,此时可以悔婚回到 Free)
- Married(最终的结果,在最后所有人都会同时进入到这个阶段)
当所有人都进入到 engaged 这个阶段时,就会停下来,此时就是最后的结果,就不会再有异动了,最后再将所有人的状态切换为 married。
伪代码如下
# Gale-Shapley
initialize each person to be free
while (some man m is free and hasn't proposed to every woman) do
w = highest ranked woman in m's list to whom m has not yet proposed
if (w is free) then
(m, w) become engaged
else if (w prefers m to her fiance m') then
(m, w) become engaged
m' become free
return the set S of engaged pairsGolang 实现版本
package main
import "fmt"
type Person struct {
name string
preferences []string
partner *Person
index int
}
// 选择更加心仪的男生
func (woman *Person) prefers(man *Person) bool {
for _, name := range woman.preferences {
if name == man.name { // 遍历到该男生同意该男生的求婚
return true
}
if name == woman.partner.name { // 当前心仪列表中的男生已经是自己的伴侣,不再考虑新来男生的求婚
return false
}
}
return false
}
func GaleShapley(men, women []*Person) {
initiallyFreeMen := make([]*Person, len(men))
copy(initiallyFreeMen, men)
for len(initiallyFreeMen) > 0 {
currentMan := initiallyFreeMen[0]
currentWomanName := currentMan.preferences[currentMan.index]
currentWoman := findPersonByName(women, currentWomanName)
// 严格代码需要判断 currentWoman 是否为 nil
if currentWoman.partner == nil {
currentMan.partner = currentWoman
currentWoman.partner = currentMan
initiallyFreeMen = removePerson(initiallyFreeMen, currentMan)
} else if currentWoman.prefers(currentMan) {
initiallyFreeMen = append(initiallyFreeMen, currentWoman.partner)
currentMan.partner = currentWoman
currentWoman.partner = currentMan
initiallyFreeMen = removePerson(initiallyFreeMen, currentMan)
} else {
currentMan.index++
}
}
}
func removePerson(people []*Person, person *Person) []*Person {
index := -1
for i, p := range people {
if p == person {
index = i
break
}
}
if index == -1 {
return people
}
return append(people[:index], people[index+1:]...)
}
func findPersonByName(people []*Person, name string) *Person {
for _, person := range people {
if person.name == name {
return person
}
}
return nil
}主要执行逻辑
func main() {
// 男生: Xavier、Yancey、Zeus
// 女生: Amy、Bertha、Clare
// 创建人员列表
xavier := &Person{
name: "Xavier",
preferences: []string{"Amy", "Bertha", "Clare"},
partner: nil,
index: 0,
}
yancey := &Person{
name: "Yancey",
preferences: []string{"Bertha", "Amy", "Clare"},
partner: nil,
index: 0,
}
zeus := &Person{
name: "Zeus",
preferences: []string{"Amy", "Bertha", "Clare"},
partner: nil,
index: 0,
}
amy := &Person{
name: "Amy",
preferences: []string{"Yancey", "Xavier", "Zeus"},
partner: nil,
index: 0,
}
bertha := &Person{
name: "Bertha",
preferences: []string{"Xavier", "Yancey", "Zeus"},
partner: nil,
index: 0,
}
clare := &Person{
name: "Clare",
preferences: []string{"Xavier", "Yancey", "Zeus"},
partner: nil,
index: 0,
}
men := []*Person{xavier, yancey, zeus}
women := []*Person{amy, bertha, clare}
// 运行Gale-Shapley算法
GaleShapley(men, women)
// 打印配对结果
for _, man := range men {
fmt.Printf("%s -- %s\n", man.name, man.partner.name)
}
}运行结果如下:
Xavier -- Amy
Yancey -- Bertha
Zeus -- Clare我们来看看这段 procedure 的流程,首先初始化所有人都为自由身(free 的状态)。接着开始进行迭代,迭代的终止条件为没有自由身的男生,也就是每位男生都找到了一个对象,迭代中找到一位为 free 的男生,并从他的喜好排序中找到最高位还没有被追求过的女生。如果女生是 free 状态,则直接答应求婚(状态变为 engaged),因为女生是可以反悔的,所以先同意这次求婚没有太大的损失,但如果这位女生已经是 engaged 的状态,就会将她的未婚夫与这位求婚的男士做对比,若她接受这位向她求婚的男生,就将他们配为新的一对,将其未婚夫变为 free 的状态,直到所有男生都不是 free 的状态,结束迭代。
分析
这个 procedure 是以男生为主动,女生可以选择答应或者拒绝,以这样的角度来说,对于男生是比较有优势的,对于女生来说她只能等着被人追求,是属于比较悲观的一方,这个 procedure 在 1962 年被创造出来时是为了解决大学生选择专业的一个制度。
证明
这个过程是否有成为算法的条件,下面会证明
- Termination(终止条件):至少在 $n^2$ 之后停止迭代
- Perfection(完美性):每个人最终都有配对的对象
- Stability(稳定性):由于是双方自己选择的结果,所以是最终稳定的
这个过程还有几个上面提到的特性:
- Male-optimal and female-pessimal:男生为最佳结果,女生属于被东悲观的结果。
- All executions yield the same matching:在相同的input 条件下,每次迭代的结果都会相同。
通常证明都是通过 “反证法” 或者 “数学归纳法” 来证明是否足以符合条件,接下来是通过反证法来证明各种条件。
Termination
# Gale-Shapley
initialize each person to be free
while (some man m is free and hasn't proposed to every woman) do
w = highest ranked woman in m's list to whom m has not yet proposed
if (w is free) then
(m, w) become engaged
else if (w prefers m to her fiance m') then
(m, w) become engaged
m' become free
return the set S of engaged pairs从上面的第 4 行可以看到,每次迭代都会有一个男生向女生求婚,并且一定会产生一组匹配,因为只要女生是 free 的,她就一定会先同意,就算她已经处于订婚状态,如果她反悔当前配对数量也是保持不变,只是对象换了,所以最终在 $n^2$ 之后一定会停止迭代。
可以发现,男生都是从最喜欢的女生开始选择,而女生可能通常是反方向且被动的与求婚者订婚,可能自己喜欢的男生被其他女生劫胡了。
Perfection
# Gale-Shapley
initialize each person to be free
while (some man m is free and hasn't proposed to every woman) do
w = highest ranked woman in m's list to whom m has not yet proposed
if (w is free) then
(m, w) become engaged
else if (w prefers m to her fiance m') then
(m, w) become engaged
m' become free
return the set S of engaged pairs从第三行来看,若最终有一个男生没有找到对象,那么循环将一直持续下去,只有所有的男生都找到对象,这个循环才会结束。
Stability
Stable matching 的最后结果是唯一的,因为只要不改变男女互相喜欢的 ranking 顺序,就不会得到不同的结果,即便改变了男生表白的顺序。
比如上面的运行结果是 Xavier <-> Amy 、Yancey <-> Bertha、Zeus <-> Clare 这三个匹配结果。
现在我们打乱他们的求婚顺序,让 Zeus 先求婚再是 Yancey,最后才是 Xavier 。接下来看看结果
Zeus -- Clare
Yancey -- Bertha
Xavier -- Amy可以看到运行结果没有变化。
拓展
现在有了这个匹配算法,可以做什么事呢?比如 CDN 调度,资源分配就可以利用这个算法,比如将各地区的流量分配至各地区的节点,节点可以承接流量。而且为了 95 水位的稳定,还需要一个省的流量不要经常变动。这就需要稳定匹配算法了。