最短路径算法是一个比较常见的用于查找2点之间最短路径的方案。在工作中，由于涉及要查找2点之间的最短路径的场景，所以特此记录一下
算法思想
美国应用数学家Richard Bellman (理查德.贝尔曼, 动态规划的提出者)于1958 年发表了该算法。此外Lester Ford在1956年也发表了该算法。因此这个算法叫做Bellman-Ford算法。
Bellman-Ford算法是一种基于逐次逼近思想进行最短路径求解的算法。其可以被应用在带负权的有向图中，Bellman-ford 算法比dijkstra算法更具普遍性，因为它对边没有要求，可以处理负权边与负权回路。缺点是时间复杂度过高，高达O(VE), V为顶点数，E为边数。
其核心思想为：对于任意一个具有n个节点的图 𝐺 ，任意两点之间的最短路径至多包含 𝑛−1 条边。因此我们可以反复通过对边的松弛来得到当前图的最短路径。
也就是说：第1轮在对所有的边进行松弛后，得到的是源点最多经过一条边到达其他顶点的最短距离；第2轮在对所有的边进行松弛后，得到的是源点最多经过两条边到达其他顶点的最短距离；第3轮在对所有的边进行松弛后，得到的是源点最多经过一条边到达其他顶点的最短距离……
松弛操作的含义是更新节点之间的最短距离。
分析
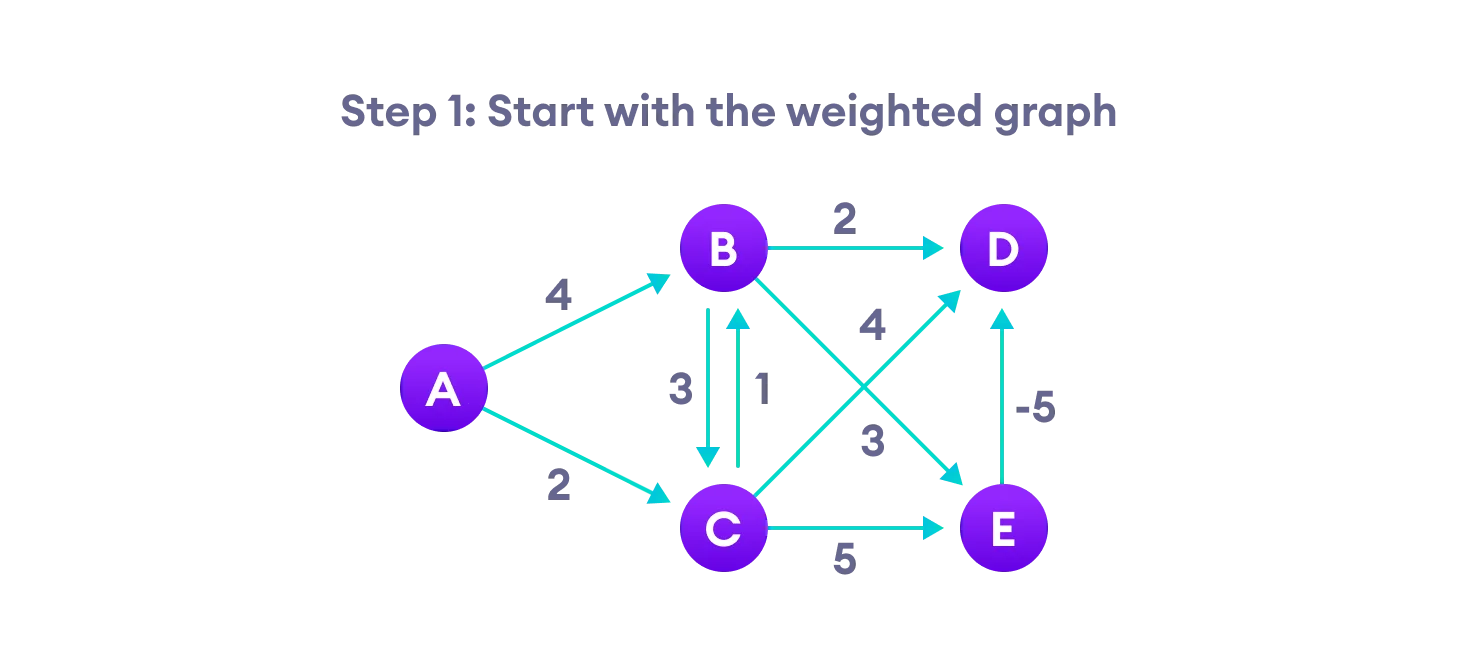
第一步：创建一个带权重 (可以有负权) 的有向图
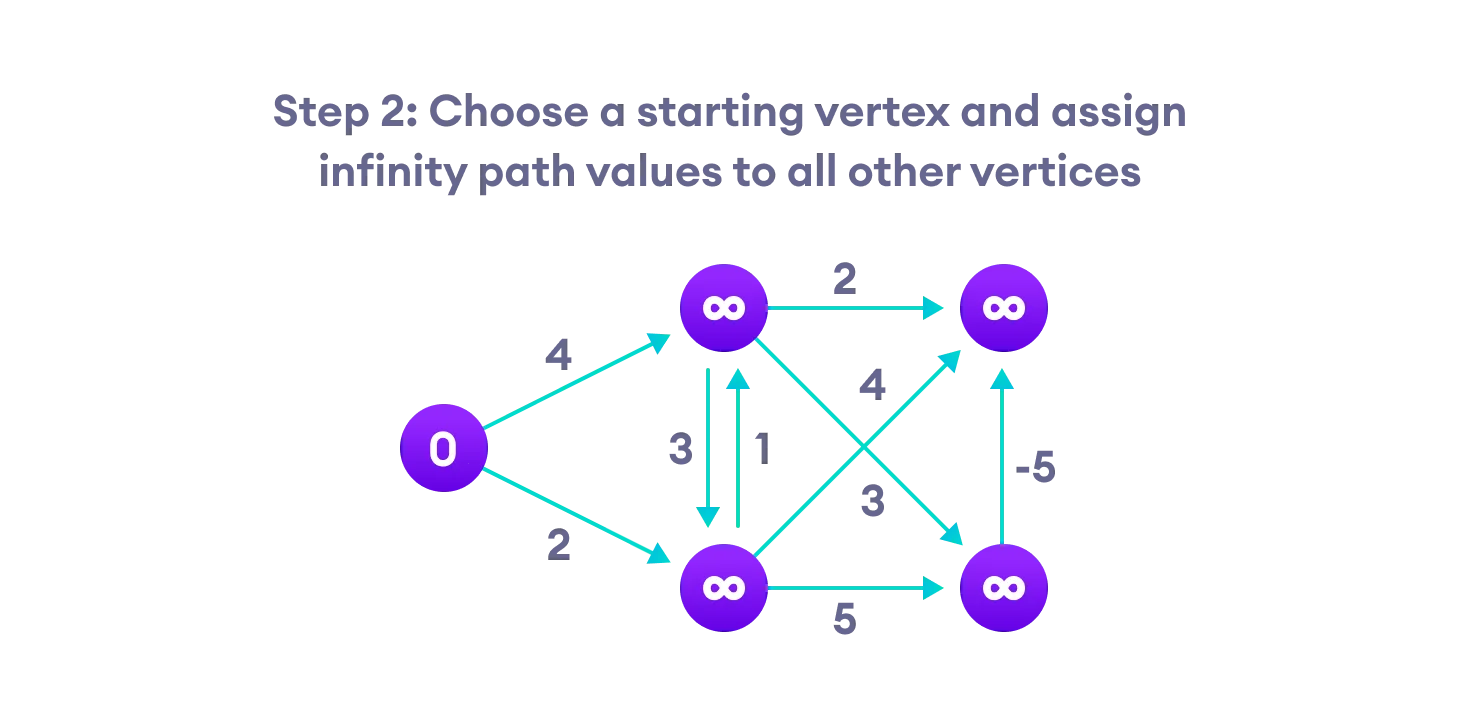
第二步：选定一个起点（A），将A 到所有节点的 距离都置为 无穷大。
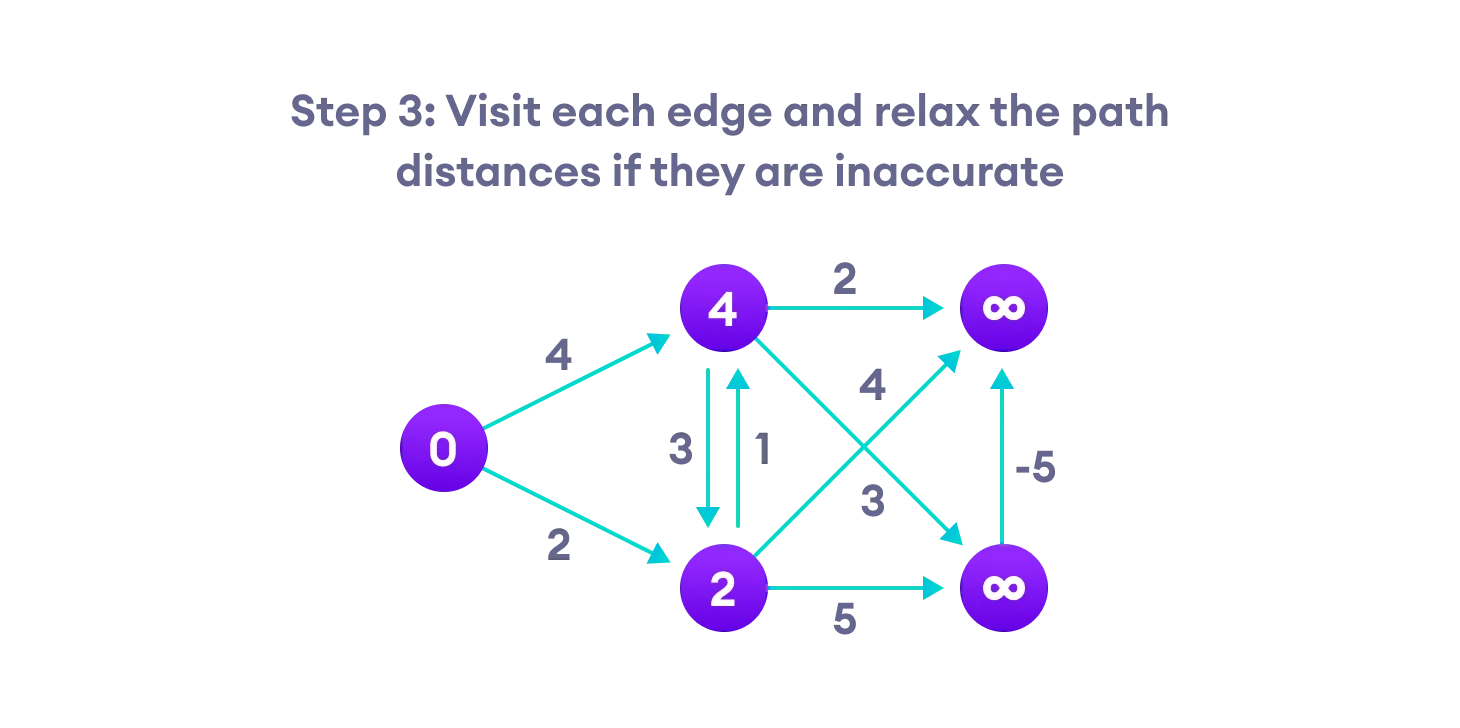
第三步：从节点A开始，将节点最短距离更新，比如 A -> B 直接相连，最短距离是 4 ，A->C 直接相连，距离是 2 。
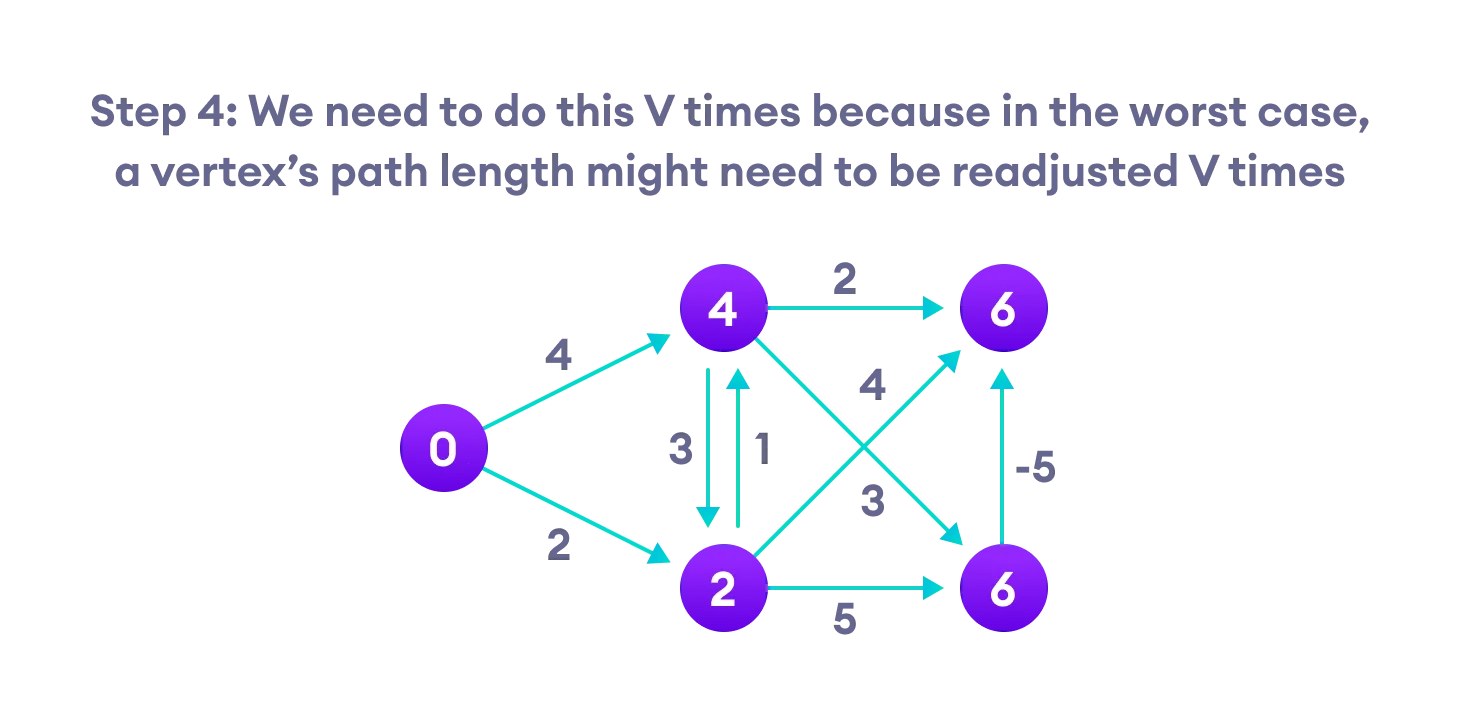
第四步：最差的情况下，我们需要 V （节点个数）次这样的操作。一个节点最短路径需要被调整 V 次。
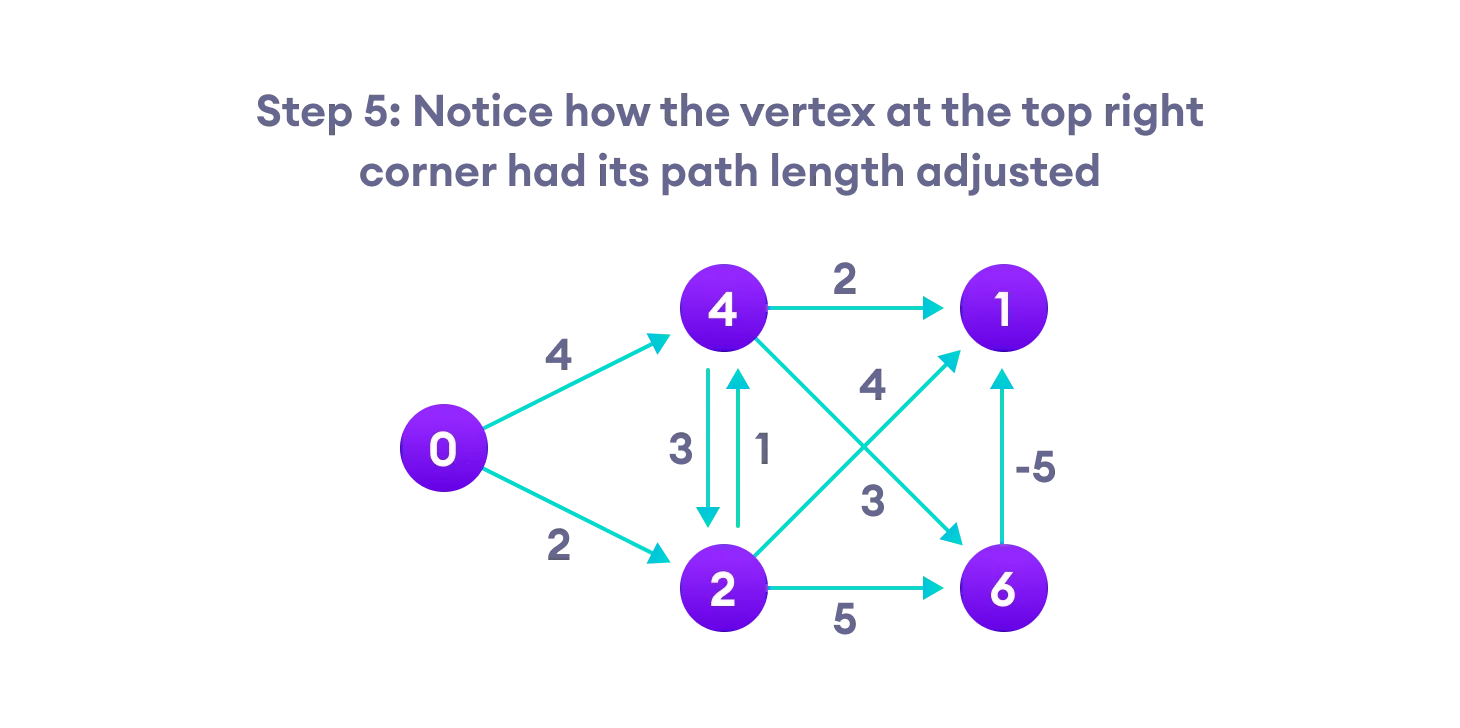
第五步：注意右上角的节点 D 是怎么调整的，因为 B -> D (4+2) = 6 , C -> D (2+4) =6 , E->D (6-5)=1 ，所以被更新.
第五步：经过最大循环次数 or 所有的顶点都有其路径长度且不再变后，检查是否有负循环。
负环的含义
短路径算法通常用于在加权图中找到两个顶点之间的最短路径。然而，当图中存在负权边时，情况就会变得复杂。负权环（Negative Weight Cycle）是指图中的一个环，其总权重为负值。如果存在负权环，那么最短路径的概念可能会变得模糊，因为你可以无限次地通过这个环来减少路径的总权重。
负权环的存在可能导致算法无法正确工作，因为它们可能会陷入无限循环。例如，贝尔曼-福特算法（Bellman-Ford）在存在负权环的情况下可以检测到问题，但无法找到最短路径。而像迪杰斯特拉算法（Dijkstra’s algorithm）这样的算法则可能给出错误的结果，因为它们假设权重非负。
这里是一个简单的图示来解释负权环：
1
| A --1--> B --2--> C --(-3)--> A
|
在这个图中，A到B是1的权重，B到C是2的权重，而C回到A有一个权重为-3的边。这个图中存在一个负权环：A -> C -> A。如果我们从A出发，经过C再回到A，总权重是-3。如果我们重复这个过程，路径的总权重可以无限减小。
参考：https://www.geeksforgeeks.org/bellman-ford-algorithm-dp-23/
Golang 实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
| type Edge struct {
src int
dest int
weight float64
}
type Graph struct {
vertices int
edges []Edge
}
func InitGraph(vertices int) *Graph {
return &Graph{
vertices: vertices,
edges: make([]Edge, 0),
}
}
func (g *Graph) AddEdge(src, dest int, weight float64) {
g.edges = append(g.edges, Edge{src, dest, weight})
}
func BellmanFord(g *Graph, source int) ([]float64, []int) {
dist := make([]float64, g.vertices)
prev := make([]int, g.vertices)
for i := 0; i < g.vertices; i++ {
dist[i] = math.Inf(1) // 将所有节点的距离设为 无穷大
prev[i] = -1 // 保存到节点v最短距离，到v的上一跳是哪个节点
}
dist[source] = 0 // 起点的距离为 0
// Relax edges V - 1 times（i 从 1 开始计数）
for i := 1; i < g.vertices; i++ {
for _, edge := range g.edges {
u := edge.src
v := edge.dest
w := edge.weight
if dist[u]+w < dist[v] {
dist[v] = dist[u] + w
prev[v] = u
}
}
}
// Check for negative cycle，经过了 v-1 次循环了，还是存在更短的路径证明存在负环了
for _, edge := range g.edges {
u := edge.src
v := edge.dest
w := edge.weight
if dist[u]+w < dist[v] {
fmt.Println("Graph contains a negative weight cycle")
return nil, nil
}
}
return dist, prev
}
func PrintShortestPaths(dist []float64, prev []int, source int) {
fmt.Println("Shortest Paths from vertex", source)
for i := 0; i < len(dist); i++ {
if dist[i] == math.Inf(1) {
fmt.Printf("Vertex %d is not reachable\n", i)
} else {
path := []int{}
j := i
for j != -1 {
path = append([]int{j}, path...)
j = prev[j]
}
fmt.Printf("Vertex %d: Distance=%f, Path=%v\n", i, dist[i], path)
}
}
}
func main() {
g := InitGraph(5)
g.AddEdge(0, 1, 1)
g.AddEdge(0, 2, 1)
g.AddEdge(1, 2, 1)
g.AddEdge(1, 3, 1)
g.AddEdge(1, 4, 1)
g.AddEdge(2, 3, 1)
g.AddEdge(2, 4, 1)
g.AddEdge(3, 1, 1)
g.AddEdge(4, 0, 1)
g.AddEdge(4, 3, 1)
source := 0
dist, prev := BellmanFord(g, source)
if dist != nil && prev != nil {
PrintShortestPaths(dist, prev, source)
}
}
|